Structures linéaires : Listes

Cours

Une liste¹ est une structure abstraite de données constituée d'éléments d'un même type, chacun possédant une position (ou rang) dans la liste.

La composition d'une liste change quand de nouveaux éléments sont ajoutés à la liste ou des éléments sont supprimés de la liste. Une liste peut éventuellement être vide.

Une liste (non vide) est composée de deux parties :

• La tête (notée car²), qui est le dernier élément ajouté à la liste ;
• La queue (note cdr³ ), qui contient le reste de la liste, elle-même une liste.

La longueur de la liste est le nombre d'éléments composant la liste. Une liste vide a une longueur zéro.

Notons ici le caractère récursif de cette définition où la queue d'une liste est elle-même une liste !

Interface

Les principales primitives constituant l'interface d'une liste sont :

• creer() → liste : construire une liste vide.
• est_vide() → bool : vérifier si une liste est vide ou non.
• inserer_tete(element) : insérer un élément en tête de la la liste.
• supprimer_tete() → element : supprimer l'élément de tête.
• taille() → int : renvoyer le nombre d'éléments de la liste.
• tete() → element : lire le premier élément (la tête) de la liste.
• queue() → liste : accéder au reste de la liste (la queue).

Il est possible d'ajouter quelques primitives supplémentaires, par exemple :

• insérer(element, i) : insérer un élément en ième position de la liste.
• lire(i) → element : accéder au ième élément de la liste (get).

Implémentation

La liste est un type abstrait, son implémentation peut se faire sous différentes formes, en particulier les tableaux et les listes chaînées.

Attention à ne pas confondre type abstrait de données liste avec le type list de Python. Le type list Python est en réalité un tableau dynamique, ce n'est qu'une forme d'implémentation particulière de la structure de données abstraite liste mais ce n'est pas la seule.

Récursive avec des tuples imbriqués

Une liste peut être implémentée sous la forme :

• d'un tuple vide (), si la liste est vide ; ou sinon
• d'un couple composé de la tête de la liste et de sa queue : (car, cdr).

Prenons par exemple une liste vide implémentée par le tuple (), et insérons l'élément 'a' en tête, la nouvelle liste obtenue est ('a', ()), sa tête est 'a' et sa queue (). Insérons maintenant un élément 'b' dans cette liste, la nouvelle liste obtenue est ('b', ('a', ())), sa tête est 'b' et sa queue ('a', ()). Puis insérons successivement les éléments 'c' et 'd', la nouvelle liste est ('d', ('d', ('b', ('a', ())))), la tête est 'd' et la queue ('d', ('b', ('a', ()))).

Ecrivons en Python ces premières primitives de liste qui permettent de créer une liste vide puis d'insérer un élément en tête de liste :

def creer():
    return ()  # renvoie une tuple vide

def est_vide(L):
    return L == ()

def inserer_tete(L, e):
    return (e, L)

ma_liste = creer()
ma_liste = inserer_tete(ma_liste, 'a')
ma_liste = inserer_tete(ma_liste, 'b')
ma_liste = inserer_tete(ma_liste, 'c')
ma_liste = inserer_tete(ma_liste, 'd')

Ajoutons quelques primitives supplémentaires :

def tete(L):
    return L[0]

def queue(L):
    return L[1]

La taille de la liste est calculée de façon récursive :

def taille(L):
    if est_vide(L):
        return 0
    else:
        return 1 + taille(queue(L))

L'affichage est aussi récursif :

def afficher(L):
    if est_vide(L):
        print('')     
    else:
        print(tete(L), end=' - ' ) 
        afficher(queue(L))

ainsi que la recherche d'un élément dans la liste :

def chercher(L, elem):
    if est_vide(L):
        return False 
    elif tete(L) == elem:
        return True 
    else:
        return chercher(queue(L) , elem) 

Avec un tableau de taille fixe

Un tableau en informatique est en général représenté par une suite de "cases mémoire", toutes de mêmes tailles, contenant les différents éléments du tableau. Une plage d'adresses mémoire est réservée afin de stocker tous les éléments.

Cette représentation présente deux avantages :

• pour un tableau sans case vide, elle est très compacte, puisqu'elle se contente de stocker les données ;

• l'accès un élément du tableau par son \(indice\) s'effectue relativement rapidement en temps constant. Son adresse se calcule facilement: \(adresseElement = adresseTableau + indice \times tailleCase\)

Implémentons en Python une liste sous forme d'un tableau de taille fixe \(n + 1\) en utilisant une variable de type list :

• la première case du tableau contient le nombre d'éléments de la liste ;
• les cases suivantes (d'indice 1 à n) contiennent les éléments de la liste ou None.

Exemple : une liste de taille 5 avec les éléments 'c', 'b', 'a' se présentera sous la forme [3, 'c', 'b', 'a', None, None].

Créons l'interface d'une telle liste :

def creer_liste(longueur):
    '''(int) - > list
    Cree une liste sous forme de tableau de taille fixe
    La première case du tableau contient le nombre d'éléments de la liste
    Les cases suivantes (d'indice 1 à n) contiennent les éléments de la liste ou None
    '''
    L = [None] * (longueur + 1)
    L[0] = 0
    return L

La primitive pour insérer un élément en tête de liste est alors :

def inserer_tete(L, elem):
    ''' Ajoute elem en tete de la liste L
    - L est une liste implémentée sous forme de tableau de taille fixe
    - elem est un element ajouté à la liste (de n'importe quel type)
    la fonction ne renvoie rien car L est modifé (le type list est muable)
    '''
    # verifions si la liste est pleine
    if L[0] == len(L) - 1: raise IndexError('La liste est déjà pleine')
    else:
        for i in range(L[0], 0, -1):
            L[i+1]= L[i]
        L[1] = elem
        L[0] += 1

A noter qu'il est inutile de renvoyer la valeur de L car c'est une variable de type list, donc muable.

inserer_tete(L, 'a')
inserer_tete(L, 'b')
inserer_tete(L, 'c')

Une fonction pour afficher la liste s'écrit :

def afficher(L):
    ''' affiche la liste L
    '''
    for i in range(1, L[0] + 1):
        print(L[i], end = "-")
    print("")

Ajoutons une primitive permettant de supprimer la tête de la liste :

def supprimer_tete(L):
    ''' supprime la tete de la liste L
    la fonction ne renvoie rien car L est modifé (le type list est muable)
    '''
    # verifions si la liste est vide
    if L[0] == 0: raise IndexError('La liste est déjà vide')
    else:
        for i in range(1, L[0] ):
            L[i]= L[i+1]
        L[L[0]] = None
        L[0] -= 1

Testons le résultat :

L = creer_liste(5)
inserer_tete(L, 'a')
inserer_tete(L, 'b')
inserer_tete(L, 'c')
inserer_tete(L, 'd')
inserer_tete(L, 'e')
afficher(L)
supprimer_tete(L)
supprimer_tete(L)
supprimer_tete(L)
afficher(L)

Il est aussi possible de rajouter quelques primitives pour :

• accéder au ième élément de la liste (get) ;
• insérer un élément en tête d'une liste ;
• insére un élément en ième position ;
• etc.

Pour aller plus loin, il est aussi possible d'écrire une classe Liste avec des méthodes similaire.

Avec le type list de Python

Dans de nombreux langages informatiques, un tableau est une structure de données de taille fixe⁴. Pour insérer des données supplémentaires, il faut créer un nouveau tableau plus grand et déplacer les éléments du premier tableau vers le second tout en ajoutant la donnée au bon endroit. C'est la notion de tableau dynamique, c'est à dire un tableau dont la taille peut varier.

Cours

En Python le type list est un tableau dynamique. C'est une forme d'implémentation particulière de la structure de données abstraite de liste (mais ce n'est pas la seule). Attention de ne pas confondre les deux termes.

Le type list en Python offre toutes les primitives de base d'une liste :

>>> L = []       # creer une liste 
>>> L == []       # est_vide()
True
>>> L.insert(0, 'a')         # inserer_tete()
>>> L.insert(0, 'b')         # inserer_tete()
>>> L.insert(0, 'c')         # inserer_tete()
>>> L.insert(0, 'd')         # inserer_tete()
>>> L.insert(0, 'e')         # inserer_tete()
>>> len(L)       # taille()
5
>>> L.pop(0)       # supprimer_tete()
'e'
>>> L[0]       # tete()
'd'
>>> L[1:]       # queue()
['c', 'b', 'a']

Notons qu'ici la tête est à la première position de L.

Le type list propose bien d'autres opérateurs que les listes : extraction d'une sous-liste (L[debut:fin]), remplacement d'un élément (L[i] = nouvelle_valeur), tri (L.sort()), retournement (L.reverse()), suppression d'un élément (L.pop(i)), application d'une fonction (map(fonction, L), etc. Néanmoins, s'il peut sembler la solution miracle à de nombreux besoins, les tableaux dynamiques ne sont pas efficaces pour insérer ou supprimer un élément en plein milieu du tableau.

Par exemple, lorsqu'une nouvelle valeur 'e' est insérée en tête d'une liste ['d', 'c', 'b', 'a'], c'est-à-dire à la première position de ce tableau Python, avec la méthode insert() :

>>> L
['d', 'c', 'b', 'a']
>>> L.insert(0, 'e')
>>> L
['e', 'd', 'c', 'b', 'a']

c'est une opération qui est en réalité très couteuse, car elle consiste à :

1. agrandir le tableau ;
2. déplacer tous les éléments du tableau d'une case vers la droite, en commençant par la fin ;
3. et enfin écrire la valeur 'e' dans la première case.

C'est donc la même chose que d'écrire :

>>> L = ['d, 'c', 'b', 'a']
>>> L.append(None)
>>> for i in range(len(L) -1, 0, -1):
...     L[i] = L[i-1]
>>> L[0] = 'e'
>>> t
['e', 'd', 'b', 'c', 'a']

Le nombre d'opérations est proportionnel à la taille du tableau. Ajouter ou supprimer le premier élément d'un tableau d'un million d'éléments nécessite près d'un million d'opérations. C'est une complexité en \(O(n)\) ⁵.

Le choix d'implémentation qui a été fait ici de placer la tête de liste en position 0 d'un tableau Python suis les implémentations précédentes, il aurait été judicieux d'inverser l'ordre de la liste dans le tableau et d'utiliser L.append('a') et L.pop() pour inserer_tete et supprimer_tete.

Avec une liste chaînée

La liste chainée apporte une solution au problème de coût d'insertion et suppression d'éléments des tableaux dynamiques. Elle servira aussi de brique de base aux structures de données de piles et de files étudiées dans la suite de ce chapitre.

Dans une liste chaînée, chaque élément de la liste est stocké dans une cellule contenant :

• l'élément ;
• un pointeur (ou référence) sur la cellule suivante ;
• éventuellement (pour les listes doublement chaînées), un pointeur sur la cellule précédente.

Voilà ce que ça donne pour représenter la liste 'c', 'b', 'a' :

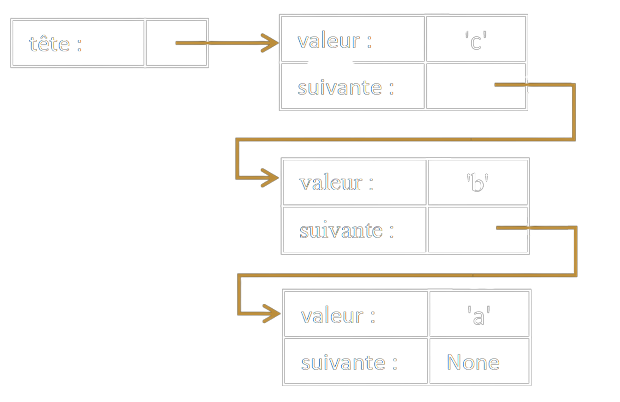
L'usage d'une liste chaînée est souvent préconisé pour des raisons de rapidité de traitement, lorsque les insertions et les suppressions d'éléments quelconques sont plus fréquentes que les accès. En effet, les insertions et les suppressions se font en temps constant car elles ne demandent au maximum que deux écritures.

Voici par exemple comment insérer l'élément 'z' entre les éléments 'c' et 'b' :

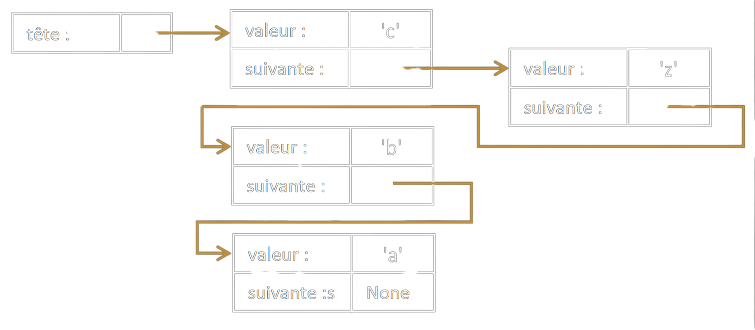
En revanche, la liste chaînée présente deux inconvénients :

• elle prend beaucoup de place, puisqu'il faut rajouter un pointeur pour chaque élément ;

• l'accès à un élément est relativement long et est proportionnel à l'indice de l'élément, puisqu'il faut parcourir la liste depuis le début (ou la fin) pour atteindre l'élément voulu.

Implémentons une telle liste chaînée en programmation orientée objet.

Commençons par la classe d'objets Cellule dont les instances ont deux attributs valeur et suivante. suivante pointe sur la cellule suivante d'une cellule ou sur None pour la dernière cellule de la liste chaînée.

class Cellule:
    ''' une cellule de liste chainee
    '''

    def __init__(self, v, s):
        self.valeur = v
        self.suivante = s 

Il est déjà possible de construire la liste 'c', 'b', 'a' :

lst = Cellule('c', Cellule('b', Cellule('a', None)))

>>> lst
<__main__.Cellule object at 0x03633BE0>

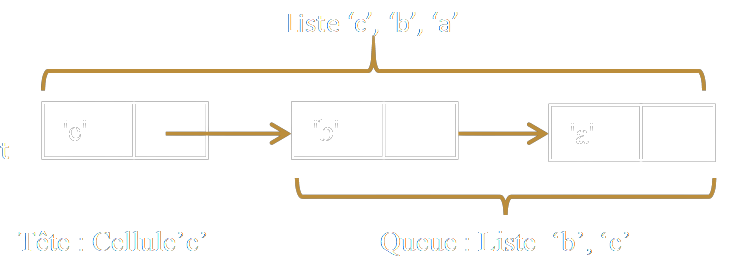
Ajoutons une méthode pour afficher la valeur d'une cellule en utilisant __str__() qui renvoie une chaine de caractère permettant d'afficher un objet avec la fonction print().

    def __str__(self):
        return 'valeur:' + self.valeur

Créons maintenant la classe ListeChainee pour représenter une liste chaînée par :

• None si la liste est vide ; ou
• une instance de Cellule qui contient la tête avec un attribut suivant qui pointe vers une autre liste, la queue.

On retrouve la défintion récursive d'une liste.

class ListeChainee:
    ''' liste chainee    '''
    def __init__(self):
        self.tete = None

et une première instance de liste chainée vide :

lst = ListeChainee()

Ajoutons immédiatement la première primitive qui vérifie si une liste est vide ou non :

    def est_vide(self):
        if self.tete is None: return True                   
        else: return False

Maintenant ajoutons une primitive pour insérer une Cellule en tête de liste :

    def inserer_tete(self, v):
        self.tete= Cellule(v, self.tete)

Comme attendu, la liste n'est plus vide :

>>> lst = ListeChainee()
>>> lst.inserer_tete('a')
>>> lst.est_vide()
False

Ajoutons les deux autres éléments à cette liste :

>>> lst.inserer_tete('b')
>>> lst.inserer_tete('c')

La longueur de la liste peut constituer un attribut privé de la classe avec un accesseur pour l'obtenir :

class ListeChainee:
    ''' liste chainee     '''
    def __init__(self):
        self.tete = None
        self._longueur = 0

    def longueur(self):
        return self._longueur

Affichons la tête de liste :

>>> print(lst.tete)
valeur:c

Une primitive get permet de lire l'élément en position n :

    def get(self, n):
        cellule = self.tete
        for i in range(n):
            cellule = cellule.suivante
        return cellule

En moyenne, s'il est immédiat de trouver l'élément de tête, il faut \(n\) opérations pour trouver le dernier élément dans une liste de longueur \(n\), donc en moyenne \(n/2\), la complexité est en \(O(n)\) ce qui est très couteux en comparaison d'un tableau dynamique.

Ajoutons une assertion sur la valeur de n dans le cas où n est supérieur à _longueur :

        assert n < self._longueur, "n doit être inférieur à la taille de la liste"

Ou alors la primitive peut renvoyer un code erreur, -1 par exmple :

        if n >= self._longueur: return -1

La méthode __str__() permet d'afficher toute la liste avec print() en parcourant toute la liste :

    def __str__(self):
        affiche = ''
        cellule = self.tete
        for i in range(self._longueur):
            affiche += cellule.valeur + ';'
            cellule = cellule.suivante
        return affiche

print (lst)

Complétons l'interface avec une primitive pour ajouter un élément en position n, (comme l'élément 'z' entre 'c' et 'b' dans l'exemple ci-dessus) :

    def inserer(self, v, n):
        if n > self._longueur: return -1
        if n == 0: self.tete = Cellule(v,self.tete)
        else:
            old = self.get_element(n - 1)
            new = Cellule(v, old.suivante)
            old.suivante = new
        self._longueur += 1

En moyenne, comme pour la recherche , un élément est ajouté immédiatement en tête de liste, et après \(n\) opérations en dernère position dans une liste de longueur \(n\), donc en moyenne après \(n/2\) opérations. La complexité est en \(O(n)\) est comparable au tableau dynamique, mais le nombre d'écritures est grandement réduit.

Pour aller plus loin, il est possible de définir une méthode pour supprimer l'élément en position n, vérifier la présence d'une valeur dans la liste, trier une liste, concaténer deux listes, etc.

Noter que cette implémentation permet de créer une liste muable (mutable en anglais) ce qui permet par exemple d'insérer un élément en tête de liste ou même au milieu.

---

1. Le langage de programmation Lisp (inventé par John McCarthy en 1958) a été un des premiers langages de programmation à introduire cette notion de liste (Lisp signifie "list processing"). ↩

2. contents of address register ↩

3. contents of decrement register ↩

4. Par exemple pour déclarer un tableau de 4 entiers en C, il faut écrire int myNumbers[4];. ↩

5. Le coût d'insertion d'un élement en début de tableau est proportionnel à la taille du tableau, ce qui peut être observé avec le module time:

   import time
   
   L = [i for i in range (100000)]  
   start = time.time()
   for i in range(100):
       L.insert(0, 0)
   end = time.time()
   print((end - start) / 1000)
   

   Pour en savoir plus sur le coût des opérations sur les listes : https://wiki.python.org/moin/TimeComplexity ↩